a topology puzzle

I want to share one of my favorite topology puzzles. It's about two pairs of handcuffs.

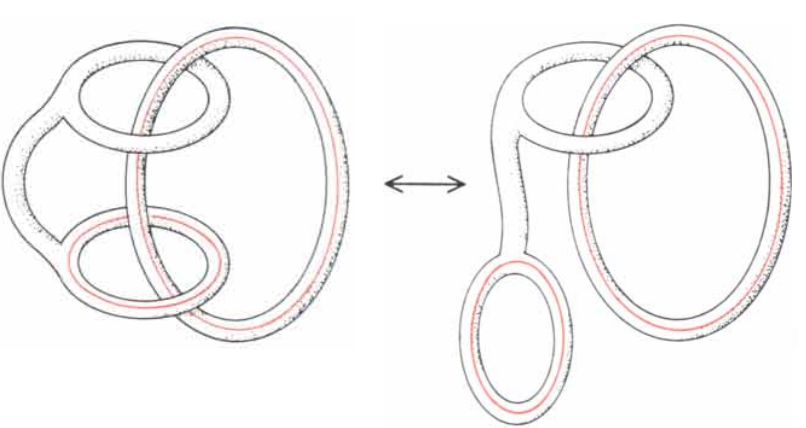
I claim that, surprisingly, these two pictures are one and the same; you can manipulate the handcuffs to change the first picture into the second and vice versa, without breaking the handcuffs open. The puzzle is: how do you do it?

This is a topology puzzle, so your can only stretch the handcuffs and circle and twist them around, as if everything was made of super-stretchy rubber, but you cannot break or rip them, or create any sharp pinches. (Formally, there is an ambient isotopy between the two pictures, like in knot theory when two knots are the same.) It's not a trick question, and the solution isn't overly complicated, but it does require thinking out of the box a bit and it probably is difficult. I'll give a little hint below.

some text so you don't see the answer

I'm now going to fill this space with some brief topology exposition, mostly so that you can stare at the picture without seeing the hint or solution until you scroll down. Feel free to not read this, if you only want to do the puzzle and not math.

For most (all?) of history, humans have been interested in shapes. People did geometry in Mesopotamia, ancient Egypt, ancient Greece, and ancient India. For example, you can look at polygons or polyhedrons and figure out many cool things about them and derive interesting formulas for them and analyze their symmetries and whatnot. But some days you look at the wikipedia page on archimedean solids and you're like "man, these are all just a bunch of funky d20s." In some sense, they're all like a sphere - they're 2D surfaces in 3D space, which enclose a single volume. But there's other shapes that are very different; for example a torus (the shape of the surface of a bagel). It's not the size or proportions which are different, but instead the structure - it has a hole in the middle in a different way than a sphere. One way to tell them apart, that comes in handy in the theory - you can draw a circle around the bagel and there's no way to shrink that circle to a point, while on a sphere any circle you draw on it can be shrunk to a point.

So we want a way to tell the "structure" of shapes apart, and classify shapes based on structure. But first, to do this, we have to figure out what counts as a shape. This sort of definition making is hard, and one good illustration of the process is Proofs and Refutations by Lakatos, which is a good read about what the mathematical proof process is like. In our case, we can come to many possible definitions: we might only care about shapes where we can measure the distance of points on them, or shapes that don't have weird fractal boundaries, or shapes that can be embedded in 3D space.

What topology cares about is much more broad, and came out of almost 200 years of generalizing. We drastically leave behind notions of distance, angles, and geometry and leave only one thing: which points are "close" to other points in the shape? Since these "shapes" in general can't be put nicely into normal Euclidean space, we consider them as spaces in their own right, not embedded in any ambient space, but just a set of points where we know some points are close to others, but we don't know how close. In the case of this puzzle, we have pretty tame shapes, embedded nicely in 3D space, so it's actually more specialized than plain old topology (point-set topology).

The axioms of topology are somewhat obtuse, defined in terms of "open sets" which capture what I mean by nearness, but despite being easy to work with the intuition can be difficult to obtain. They do lead to the notion of neighborhoods, however, which capture what it means to be near to a point. Most of modern math is done from the viewpoint that you have some type of objects you care about (sets, shapes, functions, groups), and a set of "allowed" maps between them. So in the case of topology you have spaces with points that are near to each other, and functions which preserve nearness - they map close-together points to close-together points. These allowed functions are called continuous functions---the same as the continuous functions you might meet in a calculus class, but there it's the special case where your topological space is the real numbers.

Continuous functions, by themselves, don't preserve shape: you can, for example, map a torus onto the whole of a sphere despite them being different shapes. However, you can't do it in a reversible way. If you have a continuous function from one space to another, and it has a continuous inverse function, then that does preserve shape. There is no continuous map from a torus to a sphere with continuous inverse, and so they are different shapes. This type of map, a continuous function with continuous inverse, is called a homeomorphism, and it captures the notion of stretching and twisting without breaking or ripping that this puzzle asks for.

I'm omitting a bunch of detail here - homeomorphism allows mapping one pair of handcuffs to the other continuously, but we case about the surrounding space, and we can't just teleport the handcuffs around while preserving the shape, which homeomorphism can let us do. Instead, we want to continuously deform one to the other - a notion is called isotopy. I've already written too much and haven't stated anything formal, so I had better stop here before I confuse people more.

the hint

Here's the little hint I mentioned earlier: You might be thinking that the first picture has two little circles wrapped around the big circle can't possibly change to one little circle wrapped around the big circle. It seems like an invariant, something that topology can't change. This is good intuition; you can probably do stuff with the fundamental group to prove this fact. So if it's true, then both pictures must have the same number of circles wrapped around the big circle. How can you apply this here?

the answer

Here's the solution and explanation of how I solved it.

The key insight into my solution is related to the hint I gave: in the first picture, there's two little circles linked to the big circle, so it has to stay that way. It can't get unlinked. That means the unlinked handcuff in the second picture doesn't correspond to the unlinked handcuff in the first picture at all!

In fact, there are really three loops in the handcuff we care about. Two of them are clear in both pictures, but the third one is not so easily seen. And in both pictures, we have two loops linked to the big circle, and one loop unlinked. Here's a picture below, color-coded with corresponding loops (with apologies to colorbind readers):

[TODO insert picture with loops color-coded, including outer loop]

However, we want to actually deform one to the other. To do this, I'll try deforming it so that all three loops are the same. Here's the steps I took:

[TODO insert picture with "fattened handcuff neck"]

[TODO insert picture "amoeba with two holes"]

[TODO insert picture "pretzel ring thing"]

[TODO insert picture "3D-ified pretzel ring thing"]

From here, it's straightforward (but can possibly take some effort) to see that these two pictures are the same, but rotated in 3D space.

So do this transformation, rotate, and undo the transformation, and you've stretched your way out of a prison sentence.

If you solved it differently, let me know! At some point I'll add a comment section, maybe? Also, if you'd be willing to make or help me make an 3D animation of this, please reach out. I downloaded blender and manim and gave them both a shot, but didn't have the stamina to figure out how to make it look nice.